关键词 粗糙集；区分矩阵；属性约简；区分线性表
1 引言
粗糙集(Rough Set ,RS) 理论是 Z.Pawlak 提出的一种处理不一致、不完整数据和不精确知识表达等各种不完备信息的数学理论[1] 。其中属性约简是粗糙集理论中核心内容之一，现已证明是典型的NP难题[2，3]。所谓属性约简是指在保证信息系统分类能力或决策能力不变的条件下，删除属性集中的冗余属性。属性约简在分类学习及分类数据挖掘中具有重要的作用，目前国内外学术界在属性约简方面已经做了大量研究，并得到了许多有效的算法[4~6]。文献[4] 深入分析了算法低效性的根源,给出了高效的约简算法；文献[5]给出了基于信息论的方法；文献[6]利用正区域的启发式信息给出了两种属性相对约简算法；其中应用较多的是基于华沙大学数学家Skowron提出差别矩阵[7]以及在此基础上的一些改进[9~11]，由于这种基于区分矩阵方法易于解释和计算核属性,同时也便于约简，该方法为属性约简算法提供了一种很好的思路。然而，基于区分矩阵的属性约简算法对对象数为n的区分矩阵大小为n(n-1)/2，不适用于大数据量的情况，所以本文给出了一种改进算法，将空间复杂度至少压缩到|U/R|*（|U/R|-1）/2，该算法大大降低了算法的空间复杂度，适用于大数据量的情况。
2 基本概念
定义1[2]：设U为一个有限的非空论域，R为U上的等价关系。等价关系R 把集合U 划分为多个互不相交的子集，每一个子集称为一个等价类，用[x]R表示， [x]R={y∈U| xRy}，其中x∈U，x∈y称为关于R 的等价关系，论域U上的所有等价类的集合用U/ R来表示。
定义2[2]：令R为一族等价关系，r R,如果 IND(R)= IND(R-{r}),则称r为R中不必要的；否则r为R中必要的[2]，若R中任意一个等价关系r都是必要的，则称R是独立的，否则称R是依赖的。
定义3[8]：设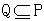 
，若Q是独立的，且IND(Q)=IND(P)，则Q是等价关系族P的一个约简。
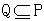，若Q是独立的，且IND(Q)=IND(P)，则Q是等价关系族P的一个约简。 定义4[8]：设P和Q是论域U上的等价关系，Q的P正域记作POSP(Q)，定义为：
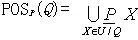
Q的P正域是U中所有根据U/P的信息准确分类到关系Q的等价关系中去的对象构成的集合。
定义5[8]：设P和Q是论域U上的等价关系，R∈P，若
POSP(Q) =POS(P-{R})(Q)
则称R为P中Q不必要的，否则称R为P中Q必要的。
若P中任意一关系R都是Q必要的，则称P是Q独立的(相对于Q独立的)。
定义6[2]：设 S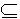
P，S为P的Q约简，当且仅当S是P的Q是独立的子集，且POSS(Q) =POSP(Q). P的Q约简称为相对约简。
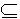P，S为P的Q约简，当且仅当S是P的Q是独立的子集，且POSS(Q) =POSP(Q). P的Q约简称为相对约简。 定义7：区分矩阵是华沙大学数学家Skowron[7]提出的，对于系统S=(U,A),其中A=C∪D, a(x)是x在属性a上的值,区分矩阵M为：
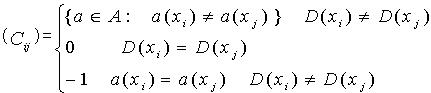
同时分辨矩阵中的核就是组合数为1的属性。
3 基于区分链表的属性约简改进算法
区分矩阵的空间复杂度为n(n-1)/2,保存着论域中两两对象的可区分属性.在论域关于属性集划分中，同一个等价类的对象两两在区分矩阵中的元素为空，而且与其他等价类的对象所构成的区分矩阵中的元素完全相同，因此从每一个等价类中只取一个对象构造的新的论域，其约简与原来的相同,而空间复杂度最多为|U/R|*（|U/R|-1）/2.
区分矩阵Matrix的某元素Matrix[i][j]，是区分对象U[i]与U[j]的条件属性集，由于在合取吸取运算中，参数i、j并没有实际价值，因此改用区分链表List来取代区分矩阵。在构造区分链表前，先定义存储核属性的变量core，可区分两对象的条件属性集若只有一个属性Ri，则属性Ri是核属性，那么Ri存储到变量core，在接下来的区分链表的构造过程中，若区分属性集包括已经提取出来的核属性，直接约去，不插入到区分链表中；否则，插入到区分链表的表尾。为减少区分链表的大小，可以在每产生一个核属性Rj，进入变量core后，化简区分链表List，若List中的元素List[k]包含属性Rj则直接删除元素List[k]。对应算法如下：
for(p=U;p->next !=NULL;p=p->next)
for(q=p->next;q!=NULL;q=q->next)
{
x= 对象p、q的可区分属性集；
if（|x|==1） 则x进入核变量core；
else if（x不包含核变量core中已有的任何一个核属性）
List.Add(x);
}
在得到了核和区分链表后，首先，将核加入到候选约简中；然后，统计区分链表中各属性出现的次数，将出现次数最多的属性R加入到侯选约简中，删除区分链表中出现R的所有节点，依次循环，直到区分链表为空，此时侯选约简就是所求约简。对应算法如下：
C_reduce=core;
While(1)
{
if(List=Null) break;
else
{
遍历List,统计各条件属性出现的次数；
选择出现次数最多的那个属性R；
C_reduce=C_reduce {R};
删除List中所有出现R的的节点；
}
}
4 实例分析
设如下表1[12]给定的决策表，求所有约简及核。
|
U
|
Conditional attributes
|
decisions
|
||
|
a
|
b
|
c
|
d
|
|
|
x1
|
2
|
2
|
0
|
1
|
|
x2
|
1
|
2
|
0
|
0
|
|
x3
|
1
|
2
|
0
|
1
|
|
x4
|
0
|
0
|
0
|
0
|
|
x5
|
1
|
0
|
1
|
0
|
|
x6
|
2
|
0
|
1
|
1
|
而应用本文给出的算法,区分线性表只有{b,c}一个元素,计算过程如下:首先得到区分属性集{a}，a进入核变量，在随后生成的区分属性集中只要含有a，则直接约掉，{b,c}进入区分线性表，采用启发式算法，可得到约简{a,b}。而基于区分矩阵的属性约简算法构造的区分矩阵如下：
本算法相对于传统方法，大大减少了区分矩阵所需要的存储空间。
5 结论
近年来Rough 集理论以其独特的优势正赢得越来越多的专家学者关注,在理论研究方面日趋成熟,并在许多领域取得了较为成功的应用，属性约简算法是粗糙集理论的核心内容之一，其中，区分矩阵作为属性约简的主要方法之一已经受到越来越多的学者关注，因此，本文深入研究分析了区分矩阵算法，基于区分线性表，提出一种改进的属性约简算法。
参考文献
[1] Pawlak Z. Rough Sets(J). International Journal of Computer and Information Science, 1982, 11(5): 341-356
[2] 张文修,吴伟志. 粗糙集理论介绍和研究综述[J ] . 模糊系统与数学,2000 ,15 (4) :1-12
[3] 王国胤. Rough 集理论与知识获取[M] . 西安:西安交通大学出版社,2001
[4] 刘少辉. Rough集高效算法的研究. 计算机学报(J), 2003,26(5):524-529
[5] 王国胤, 于 洪, 杨大春. 基于条件信息熵的决策表约简(J) . 计算机学报 ,2002, 25( 7 ): 759-766
[6] 张腾飞, 肖健梅, 王锡淮. 粗糙集理论中属性相对约简算法. 电子学报(J) ,2005, 33(11):2080-2083
[7] Skowron A. Rauszer C. The Discerni-bility Matrics and Functions in Information System(J), Intelligent Decision Support Handbook of Applications and Advances of the Rough Sets Theory Dordrecht: Kluwer Academic Publishers, 1992: 331-362
[8] 李雄飞, 李军. 数据挖掘与知识发现[M]. 高等教育出版社,2003
[9] 范 敏,刘文奇.基于粗集可辨识矩阵的属性约简算法[J ].计算机工程与应用,2004 ,38 (13) :79 - 80
[10] WANGJue ,WANGJu. Reduction Algorithm Based on Disernibility Matrix: The Ordered Attributes Method [ J ] . J . Comput . Sci . &Technol ,2001 ,16 (6) :489 - 504
[11] 王兵,陈善本.一种基于差别矩阵的属性约简完备算法[J ].上海交通大学学报,2004,38(1):43- 46
